Il segnale in elettronica
In linea generale si considera segnale una grandezza fìsica la cui variazione nel tempo risulta significativa ai fini della comunicazione di una informazione.
In elettronica sono molto usati i segnali periodici.
FIG.1
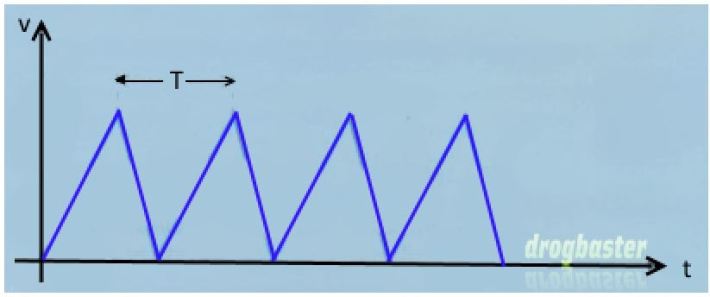
Segnale periodico
Si definisce periodico un segnale che dopo un certo intervallo di tempo torna a ripetersi ancora uguale (fig. 1).
Questo intervallo di tempo è detto periodo (T) e si misura in secondi.
// numero di periodi che si ripetono nell’unità di tempo è detto frequenza e si misura in hertz (Hz).
f = 1/T
(1)
Segnale aperiodico
Matematicamente un segnale periodico è una funzione del tempo del tipo
v(t) = v(t+nT) con n = 1, 2, 3…
(2)
I segnali privi di periodicità vengono detti aperiodici (fig. 2); questi ultimi possono però ancora considerarsi periodici con periodo T infinito.
Non si deve erroneamente pensare che nella legge di variazione dei segnali periodici sia insita l’informazione: infatti poiché questa legge è sempre la stessa non contiene alcuna informazione: che è invece presente in una eventuale variazione non prevedibile di uno o più parametri caratteristici del segnale periodico (vedere seguito paragrafo).
FIG. 2
È importante osservare che anche le grandezze costanti (in elettronica impropriamente dette continue) possono essere dei segnali anche se, per definizione, non presentando variazioni nel tempo non dovrebbero essere Segnale considerate tali. A giustificazione di questo fatto si possono fare le seguenti considerazioni:
Segnale Continuo
- Si considera normalmente continua anche una grandezza che nel tempo può subire delle lente variazioni. Si pensi, ad esempio, alla tensione fornita da un trasduttore di temperatura: il suo valore continuo può nel tempo variare in relazione alla variazione termica; in questa variazione è insita l’informazione.
- Ai fini dell’analisi del funzionamento di un circuito si procede spesso alla misura dei parametri delle grandezze elettriche presenti; anche una grandezza continua, presentando un valore variato rispetto al previsto, può quindi contenere una informazione utile.
Uso delle lettere minuscole e maiuscole
Si osservi da ultimo che nelle figure 1 e 2 si sono indicate le grandezze lettere sull’asse y con una lettera minuscola. In questo modo si vuole simboleggiare il generico valore istantaneo di una grandezza variabile nel tempo; le grandezze costanti nel tempo, al contrario, vengono indicate con lettere maiuscole.
Unità di misura
Le grandezze elettriche che vengono normalmente usate per i segnali sono la tensione che si misura in volt (V), la corrente che si misura in ampere (A) e la potenza che si misura in watt (W).
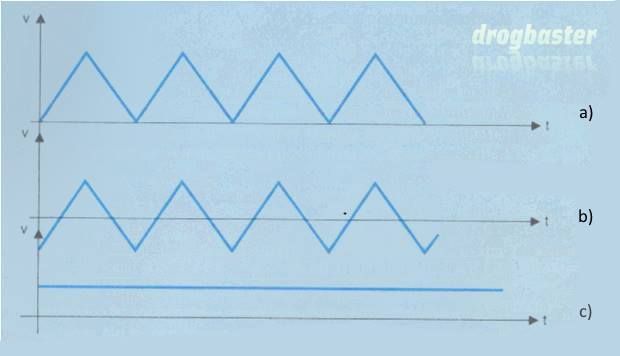
FIG.3
Mentre in elettrotecnica capita spesso di ricorrere ai multipli di queste unità di misura, in elettronica è più frequente il ricorso ai sottomultipli. Di seguito sono riportati i multipli e i sottomultipli più usati in elettronica, anche per unità di misura diverse da quelle appena nominate.
| mega | (M) | pari a 106 |
| chilo | (k) | pari a 103 |
| milli | (m) | pari a 10-3 |
| micro | (µ) | pari a 10-6 |
| nano | (n) | pari a 10-9 |
| pico | (p) | pari a 10-12 |
Esempio 3 mV = tre millesimi di volt = 0,003 V, ovvero 3-10-3 V.
10 |jA = dieci milionesimi di ampere, ovvero 10-10-6 A.
Moltiplicando la tensione per la corrente, se le grandezze sono continue, si ottiene una potenza di 3-10-3*10-10-6 = 30 nW.
Segnali Unidirezionali e Bidirezionali
Indipendentemente dalla periodicità o meno di un segnale, questo può essere unidirezionale o bidirezionale in relazione al segno che assume nel tempo la grandezza fisica.
È in particolare interessante osservare che se ad un segnale bidirezionale (fig. 3b) se ne somma uno continuo, di ampiezza opportuna (fìg. 3c), si ottiene un segnale unidirezionale (fìg. 3a).
Si può pertanto affermare che è sempre possibile considerare un segnale uni direzionale come somma di uno continuo e di uno bidirezionale.
Segnali Alternati
Si definisce alternato un segnale periodico a valore medio nullo.
Un caso particolare importante è quello sinusoidale o armonico (fig. 4).
FIG. 4
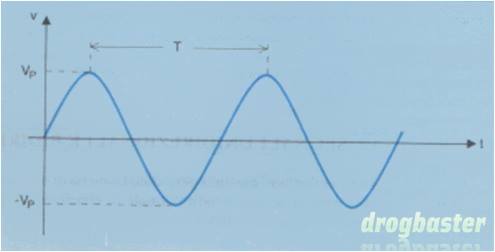
Matematicamente risulta
v(t) = VP sen (ωt + φ)
Con ω = pulsazione e φ = fase del segnale. I
Il prodotto ωt come pure φ sono degli angoli espressi in radianti.
Nel caso particolare di fig. 4 si ha φ = 0.
La frequenza, la pulsazione e il periodo non sono tra loro indipendenti:
ω = 2πf e T = 2π/ω
Valore Efficace
Un parametro molto importante, usato soprattutto con correnti e tensioni alternate, ma estendibile, per le stesse grandezze, al più generale caso periodico, è il valore efficace (root mean square = RMS).
Si definisce valore efficace di una corrente alternata il valore continuo che attraversando una resistenza provocherebbe, in un certo intervallo di tempo, lo stesso effetto termico della corrente alternata effettivamente presente nella resistenza stessa.
Poiché, come verrà meglio chiarito nel paragrafo 20, se una resistenza è attraversata da corrente ai suoi capi è presente una tensione, la definizione appena data è facilmente estendibile anche a quest’ultima grandezza. Se, ad esempio, si dice che una lampadina è alimentata con una tensione alternata di 220 Veff si intende dire che la corrente che attraversa la lampadina provoca, in un certo intervallo di tempo, lo stesso effetto termico che si otterrebbe alimentando la lampadina stessa con una tensione continua di 220 V.
Alcuni segnali Tipici
Di seguito sono riassunte le caratteristiche di alcuni segnali periodici particolarmente significativi.
Segnale armonico
FIG.5
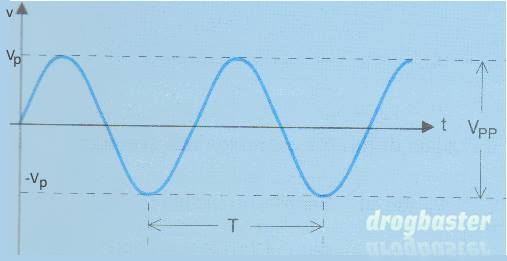
Vp = valore di picco o massimo.
Vpp = 2 Vp= valore picco-picco.
Veff = Vp/√2
Trattandosi di un segnale alternato il valore medio è nullo.
Analiticamente il segnale armonico è definito dalla (3).
La (5) non viene giustificata e altrettanto avverrà nel seguito di questo paragrafo per successive relazioni analoghe.
In fig. 6 è riportato un segnale di tipo armonico, raddrizzato a semionda; si tratta di un segnale unidirezionale e, come tale, a valore medio diverso da zero.
In fig. 7 è riportato il caso di segnale armonico raddrizzato a doppia semionda; si noti che il periodo indicato è quello del segnale sinusoidale da cui si suppone venga ricavato quello raddrizzato; il periodo di quest’ultimo è ovviamente la metà.
Segnali raddrizzati
FIG. 6 – FIG. 7
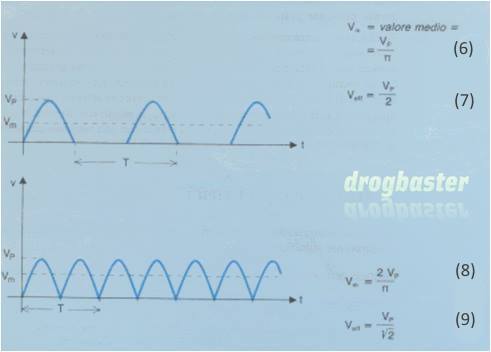
Analiticamente il segnale di fig. 6 è espresso dalla seguente funzione:
(10)
v(t) = Vp sen ωt per nT <t<(1 +2n)T/2
0 per (1 +2n)T/2<t<(1 +n)T
con n = 0, 1, 2, 3…
Il segnale di fig. 7 è espresso invece dalla:
(11)
V(t) = Vp sen ωt per nt<t<(1+2n)T/2
Vp sen ω (t-T/2) per (1+2n)T/2<t<(1+n)T
con n = 0, 1, 2, 3…
In fig. 8 è riportato un segnale alternato triangolare, in fig. 9 un segnale triangolare unidirezionale.
Segnali triangolari
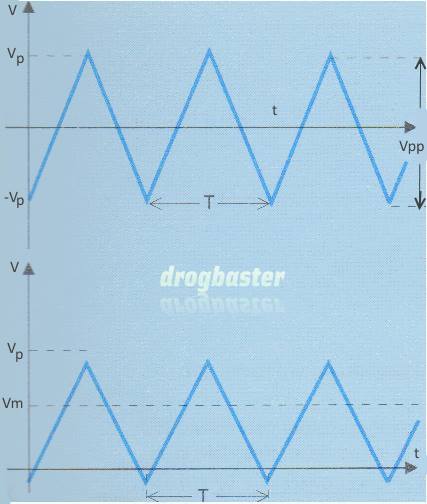
II segnale di fig. 8 è espresso dalla:
(15)
v(t) = -Vp + 4Vp/T (t- nT) per nT<t<(1+2n)T/2
v(t) = +Vp – 4Vp/T (t- T/2- nt) per (1 +2n)T/2<t<(1+n)T
con n = 0, 1, 2, 3…
L’espressione analitica del segnale di fig. 9 è facilmente ricavabile dalla ricordando che un segnale unidirezionale può sempre essere interpretato come somma di uno bidirezionale e di uno continuo.
Vm = Vp/2
(16)
Veff = Vp/√3
(17)
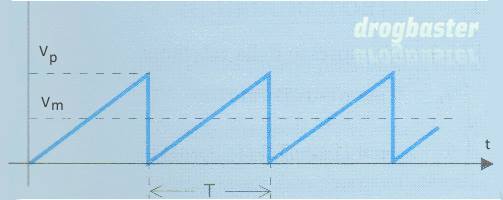
La fig. 10 riporta un particolare segnale triangolare detto a dente di sega.
Segnali a due livelli

In fig. 11 è riportato un segnale a due livelli a valore medio nullo; i due livelli hanno la stessa durata: si parla in questo caso di segnale a onda quadra.
In fig. 12 si considera un segnale a due livelli di pari durata, ma con valore medio diverso da zero; si parla ancora di segnale quadro a causa appunto della pari durata dei due livelli.
Analiticamente il segnale di fig. 11 è espresso dalla seguente relazione:
(21)
v(t) = Vp per nT<t<(1 +2n)T/2
v(t) = -Vp per (1+2n)T/2<t<(1+n)T
con n = 0, 1, 2, 3…
Il segnale di fig. 12 è invece espresso dalla relazione:
(22)
VP per nT<t<(1+2n)T/2 per
v(t) = Vp per nT<t<(1 +2n)T/2
v(t) = 0 per(1+2n)T/2<t<(1+n)T
con n = 0, 1, 2, 3…
Segnale impulsivo e duty cycle
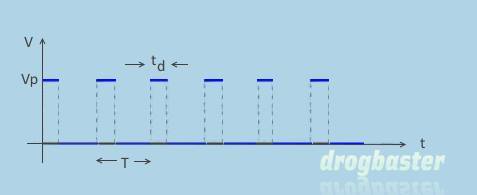
Se i due livelli hanno una durata diversa (fig. 13), si parla di segnale impulsivo.
Un parametro molto importante per i segnali a due livelli è il duty cycle (ciclo utile), definito come il rapporto percentuale tra il tempo di durata
del livello alto (basso) e il tempo di ripetizione.
D = td/T
(23)
Spesso questo parametro risulta espresso in forma percentuale.
Se il segnale a due livelli presenta un ciclo utile del 50% è un’onda quadra, altrimenti è impulsivo.
Se td, come in fig. 13, si riferisce alla durata del livello alto si parla di impulsi positivi (nel nostro esempio D<50%), se si riferisce alla durata del livello basso si parla di impulsi negativi.
Il segnale può essere generato artificialmente un circuito elettronico ( oscillatore ).
Tuttavia, nella maggior parte delle applicazioni pratiche, il segnale elettrico rappresenta la variazione di un'altra grandezza fisica nel tempo, convertita in energia elettrica da un trasduttore.
Per misurare le caratteristiche del segnale, come: il valore di picco, RMS , periodo, frequenza, ecc; è necessario l'utilizzo di un'oscilloscopio
© riproduzione riservata
ultimo aggiornamento: 03 Giugno 2016
